Thanh Nam
Guest
Tìm kiếm nhị phân
Interpolation Search là một giải thuật tìm kiếm nhanh, một biến thể cải tiến của tìm kiếm nhị phân (Binary Search). 2 giải thuật tìm kiếm này đều dựa trên nguyên tắc chia để trị (Divide and Conquer). Để giải thuật thực hiện được thì mảng đầu vào cần phải được sắp xếp sẵn từ trước.
Để hiểu về tìm kiếm nội suy, trước tiên chúng ta tìm hiểu Binary Search nhé.
Tìm kiếm nhị phân sẽ tìm kiếm một phần tử cụ thể bằng cách so sánh phần tử cần tìm với phần tử ở vị trí giữa (theo chỉ số) của mảng đầu vào:
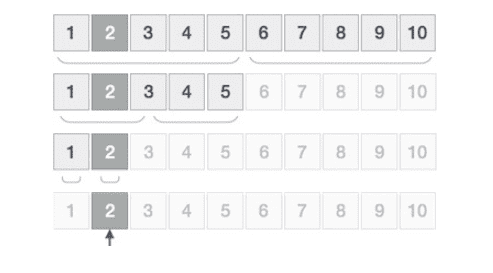
Ở ví dụ trên, chúng ta tìm kiếm giá trị 2 trong mảng số từ 1 đến 10. Sẽ có 4 vòng lặp được thực hiện để tìm ra được giá trị cần tìm.
https://topdev.vn/blog/pure-function-trong-javascript/
Tìm kiếm nội suy
Ở trong ví dụ của tìm kiếm nhị phân chúng ta thấy rằng giải thuật không quan tâm đến giá trị đầu vào và luôn luôn chia đều mảng thành 2 phần bằng nhau. Thực tế nếu chúng ta đánh giá mảng số đầu vào cùng giá trị tìm kiếm thì có thể nhận thấy giá trị 2 sẽ có nhiều khả năng nằm ở vị trí đầu của mảng số vì nó gần hơn với giá trị bé nhất của mảng là 1 hơn là giá trị lớn nhất của mảng là 10. Nó cũng giống như việc khi chúng ta tra cứu từ điển, nếu cần tra cứu từ “Interpolation” thì chúng ta sẽ ưu tiên mở phần đầu của quyển từ điển hơn (do chữ cái I nằm gần đầu trong bảng chữ cái, cũng là thứ tự sắp xếp của quyển từ điển); ngược lại khi tra cứu từ “Search” thì ưu tiên sẽ là mở đến những trang gần cuối hơn.
Từ ý tưởng này, tìm kiếm nội suy cải tiến tìm kiếm nhị phân bằng cách tính toán trước vị trí dò trong mảng dựa trên giá trị cần tìm theo công thức:
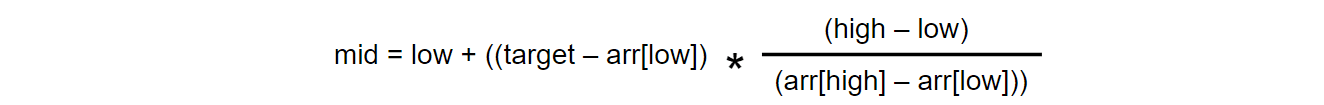
Trong đó:
Cho mảng số đã được sắp xếp như dưới đây, chúng ta cần tìm kiếm giá trị 18 trong mảng.
Tìm kiếm nội suy sẽ thực hiện các vòng lặp, với mỗi vòng lặp chúng ta có 2 bước như sau:
Bước 1: Tính toán chỉ số mảng cần so sánh theo công thức
Bước 2: So sánh giá trị cần tìm và phần tử trong mảng theo chỉ số tính toán
Với bài toán trên, giải thuật tìm kiếm nội suy sẽ cần chạy qua 2 vòng lặp như dưới đây:
Vòng lặp đầu tiên, theo công thức thì mid sẽ cho giá trị được làm tròn là
mid = 0 + (18 – 10) * (14 – 0) / (47 – 10) = 3
và phần tử trong mảng đưa ra để so sánh là giá trị 16. Do 16 < 18 (giá trị cần tìm) => mảng mới sử dụng sẽ bắt đầu từ 18 (vị trí phần tử thứ 4)
Vòng lặp thứ 2,
mid = 4 + (18 – 18) * (14 – 4) / (47 – 18) = 0
Kết quả trả về đúng giá trị cần tìm ở vị trí thứ 4 của mảng.
Độ phức tạp của thuật toán
Tìm kiếm nội suy có độ phức tạp là O(log(log
)) so với tìm kiếm nhị phân với độ phức tạp là O(log) thì việc cải tiến này khá đáng giá. Giải thuật cũng sẽ hiệu quả hơn với những bài toán mà các phần tử trong mảng được phân bố đều.
Kết bài
Như vậy là chúng ta đã cùng nhau tìm hiểu thuật toán tìm kiếm nội suy Interpolation Search và cách triển khai thuật toán này trong ngôn ngữ lập trình JavaScript. Đây là một thuật toán hay và cũng dễ triển khai trong nhiều ngôn ngữ lập trình khác nhau. Hy vọng bài viết hữu ích dành cho bạn và hẹn gặp lại trong các bài viết tiếp theo của mình.
Interpolation Search là một giải thuật tìm kiếm nhanh, một biến thể cải tiến của tìm kiếm nhị phân (Binary Search). 2 giải thuật tìm kiếm này đều dựa trên nguyên tắc chia để trị (Divide and Conquer). Để giải thuật thực hiện được thì mảng đầu vào cần phải được sắp xếp sẵn từ trước.
Để hiểu về tìm kiếm nội suy, trước tiên chúng ta tìm hiểu Binary Search nhé.
Tìm kiếm nhị phân sẽ tìm kiếm một phần tử cụ thể bằng cách so sánh phần tử cần tìm với phần tử ở vị trí giữa (theo chỉ số) của mảng đầu vào:
- Nếu bằng nhau => trả về kết quả tìm kiếm
- Nếu phần tử cần tìm lớn hơn => thực hiện lặp lại bước trên với mảng con ở bên phải phần tử ở giữa
- Nếu phần tử cần tìm nhỏ hơn => thực hiện lặp lại bước trên với mảng con ở bên trái phần tử ở giữa
Ở ví dụ trên, chúng ta tìm kiếm giá trị 2 trong mảng số từ 1 đến 10. Sẽ có 4 vòng lặp được thực hiện để tìm ra được giá trị cần tìm.
https://topdev.vn/blog/pure-function-trong-javascript/
Tìm kiếm nội suy
Ở trong ví dụ của tìm kiếm nhị phân chúng ta thấy rằng giải thuật không quan tâm đến giá trị đầu vào và luôn luôn chia đều mảng thành 2 phần bằng nhau. Thực tế nếu chúng ta đánh giá mảng số đầu vào cùng giá trị tìm kiếm thì có thể nhận thấy giá trị 2 sẽ có nhiều khả năng nằm ở vị trí đầu của mảng số vì nó gần hơn với giá trị bé nhất của mảng là 1 hơn là giá trị lớn nhất của mảng là 10. Nó cũng giống như việc khi chúng ta tra cứu từ điển, nếu cần tra cứu từ “Interpolation” thì chúng ta sẽ ưu tiên mở phần đầu của quyển từ điển hơn (do chữ cái I nằm gần đầu trong bảng chữ cái, cũng là thứ tự sắp xếp của quyển từ điển); ngược lại khi tra cứu từ “Search” thì ưu tiên sẽ là mở đến những trang gần cuối hơn.
Từ ý tưởng này, tìm kiếm nội suy cải tiến tìm kiếm nhị phân bằng cách tính toán trước vị trí dò trong mảng dựa trên giá trị cần tìm theo công thức:
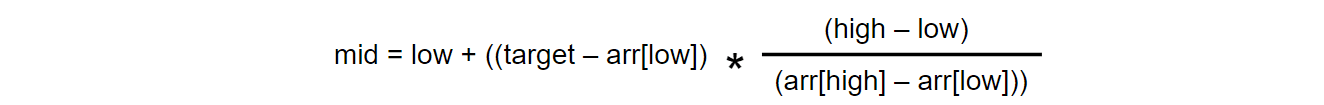
Trong đó:
- arr: mảng giá trị cần tìm kiếm
- low: chỉ mục thấp nhất của mảng
- high: chỉ mục cao nhất của mảng
- target: giá trị cần tìm kiếm
- mid: chỉ số tính toán được để thực hiện so sánh
Cho mảng số đã được sắp xếp như dưới đây, chúng ta cần tìm kiếm giá trị 18 trong mảng.
Tìm kiếm nội suy sẽ thực hiện các vòng lặp, với mỗi vòng lặp chúng ta có 2 bước như sau:
Bước 1: Tính toán chỉ số mảng cần so sánh theo công thức
Bước 2: So sánh giá trị cần tìm và phần tử trong mảng theo chỉ số tính toán
- Nếu bằng nhau => trả kết quả đầu ra
- Nếu phần tử của mảng có giá trị lớn hơn giá trị cần tìm => thực hiện lặp với mảng con bên trái
- Nếu phần tử của mảng có giá trị nhỏ hơn giá trị cần tìm => thực hiện lặp với mảng con bên phải
Với bài toán trên, giải thuật tìm kiếm nội suy sẽ cần chạy qua 2 vòng lặp như dưới đây:
Vòng lặp đầu tiên, theo công thức thì mid sẽ cho giá trị được làm tròn là
mid = 0 + (18 – 10) * (14 – 0) / (47 – 10) = 3
và phần tử trong mảng đưa ra để so sánh là giá trị 16. Do 16 < 18 (giá trị cần tìm) => mảng mới sử dụng sẽ bắt đầu từ 18 (vị trí phần tử thứ 4)
Vòng lặp thứ 2,
mid = 4 + (18 – 18) * (14 – 4) / (47 – 18) = 0
Kết quả trả về đúng giá trị cần tìm ở vị trí thứ 4 của mảng.
Độ phức tạp của thuật toán
Tìm kiếm nội suy có độ phức tạp là O(log(log
)) so với tìm kiếm nhị phân với độ phức tạp là O(log) thì việc cải tiến này khá đáng giá. Giải thuật cũng sẽ hiệu quả hơn với những bài toán mà các phần tử trong mảng được phân bố đều.Kết bài
Như vậy là chúng ta đã cùng nhau tìm hiểu thuật toán tìm kiếm nội suy Interpolation Search và cách triển khai thuật toán này trong ngôn ngữ lập trình JavaScript. Đây là một thuật toán hay và cũng dễ triển khai trong nhiều ngôn ngữ lập trình khác nhau. Hy vọng bài viết hữu ích dành cho bạn và hẹn gặp lại trong các bài viết tiếp theo của mình.